Low Level Programming

This section introduces a number of topics in low-level programming, in which the hardware and the compiler's representation choices are much more in view at the source code level. In comparatively high level code these topics are "abstracted away" in that the programmer can assume that the compiler does whatever is necessary on the current target machine so that their code executes as intended. That approach is not sufficient in low-level programming.

Note that we do not cover every possibility or language feature. Instead, we cover the necessary concepts, and also potential surprises or pitfalls, so that the parts not covered can be learned on your own.

Separation Principle

There is a language design principle underlying the Ada facilities intended for implementing embedded software. This design principle directly affects how the language is used, and therefore, the portability and readability of the resulting application code.

This language design principle is known as the "separation principle." What's being separated? The low-level, less portable aspects of some piece of code are separated from the usage of that piece of code.

Don't confuse this with hiding unnecessary implementation details via compile-time visibility control (i.e., information hiding and encapsulation). That certainly should be done too. Instead, because of the separation principle, we specify the low-level properties of something once, when we declare it. From then on, we can use regular Ada code to interact with it. That way the bulk of the code — the usage — is like any other Ada code, and doesn't propagate the low-level details all over the client code. This greatly simplifies usage and understandability as well as easing porting to new hardware-specific aspects. You change things in one place, rather than everywhere.

For example, consider a device mapped to the memory address space of the processor. To interact with the device we interact with one or more memory cells. Reading input from the device amounts to reading the value at the associated memory location. Likewise, sending output to the device amounts to writing to that location.

To represent this device mapping we declare a variable of an appropriate type and specify the starting address the object should occupy. (There are other ways too, but for a single, statically mapped object this is the simplest approach.) We'd want to specify some other characteristics as well, but let's focus on the address.

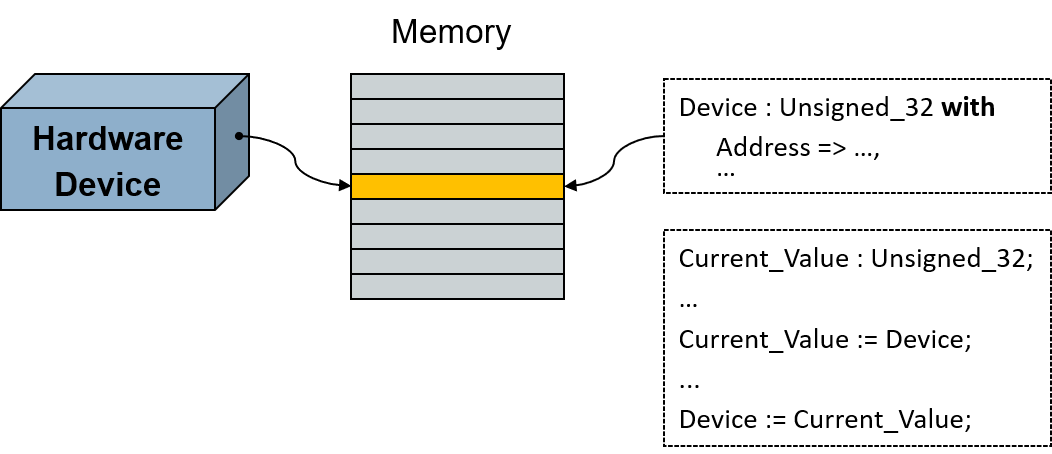
If the hardware presents an interface consisting of multiple fields within individual memory cells, we can use a record type instead of a single unsigned type representing a single word. Ada allows us to specify the exact record layout, down to the individual bit level, for any types we may need to use for the record components. When we declare the object we use that record type, again specifying the starting address. Then we can just refer to the object's record components as usual, having the compiler compute the address offsets required to access the components representing the individual hardware fields.

Note that we aren't saying that other languages cannot do this too. Many can, using good programming practices. What we're saying is that those practices are designed into the Ada way of doing it.

Guaranteed Level of Support

The Ada reference manual has an entire section dedicated to low-level programming. That's section 13, "Representation Issues," which provides facilities for developers to query and control aspects of various entities in their code, and for interfacing to hardware. Want to specify the exact layout for a record type's components? Easy, and the compiler will check your layout too. Want to specify the alignment of a type? That's easy too. And that's just the beginning. We'll talk about these facilities as we go, but there's another point to make about this section.

In particular, section 13 includes recommended levels of support to be provided by language implementations, i.e., compilers and other associated tools. Although the word "recommended" is used, the recommendations are meant to be followed.

For example, section 13.3 says that, for some entity named X, "X'Address should produce a useful result if X is an object that is aliased or of a by-reference type, or is an entity whose Address has been specified." So, for example, if the programmer specifies the address for a memory-mapped variable, the compiler cannot ignore that specification and instead, for the sake of performance, represent that variable using a register. The object must be represented as an addressable entity, as requested by the programmer. (Registers are not addressable.)

We mention this because, although the recommended levels of support are intended to be followed, those recommendations become requirements if the Systems Programming (SP) Annex is implemented by the vendor. In that case the vendor's implementation of section 13 must support at least the recommended levels. The SP Annex defines additional, optional functionality oriented toward this programming domain; you want it anyway. (Like all the annexes it adds no new syntax.) Almost all vendors, if not literally all, implement the Annex so you can rely on the recommended levels of support.

Querying Implementation Limits and Characteristics

Sometimes you need to know more about the underlying machine than is typical for general purpose applications. For example, your numerical analysis algorithm might need to know the maximum number of digits of precision that a floating-point number can have on this specific machine. For networking code, you will need to know the "endianness" of the machine so you can know whether to swap the bytes in an Ethernet packet. You'd go look in the limits.h file in C implementations, but in Ada we go to a package named System to get this information.

Clearly, these implementation values will vary with the hardware, so the package declares constants with implementation-defined values. The names of the constants are what's portable, you can count on them being the same in any Ada implementation.

However, vendors can add implementation-defined declarations to the language-defined content in package System. You might require some of those additions, but portability could then suffer when moving to a new vendor's compiler. Try not to use them unless it is unavoidable. Ideally these additions will appear in the private part of the package, so the implementation can use them but application code cannot.

For examples of the useful, language-defined constants, here are those for the numeric limits of an Ada compiler for an Arm 32-bit SoC:

Min_Int               : constant := Long_Long_Integer'First;
Max_Int               : constant := Long_Long_Integer'Last;

Max_Binary_Modulus    : constant := 2 ** Long_Long_Integer'Size;
Max_Nonbinary_Modulus : constant := 2 ** Integer'Size - 1;

Max_Base_Digits       : constant := Long_Long_Float'Digits;
Max_Digits            : constant := Long_Long_Float'Digits;

Max_Mantissa          : constant := 63;
Fine_Delta            : constant := 2.0 ** (-Max_Mantissa);

Min_Int and Max_Int supply the most-negative and most-positive integer values supported by the machine.

Max_Binary_Modulus is the largest power of two allowed as the modulus of a modular type definition.

But a modular type need not be defined in terms of powers of two. An arbitrary modulus is allowed, as long as it is not bigger than the machine can handle. That's specified by Max_Nonbinary_Modulus, the largest non-power-of-two value allowed as the modulus of a modular type definition.

Max_Base_Digits is the largest value allowed for the requested decimal precision in a floating-point type's definition.

We won't go over all of the above, you get the idea. Let's examine the more important contents.

Two of the most frequently referenced constants in System are the following, especially the first. (The values here are again for the Arm 32-bit SoC):

Storage_Unit : constant := 8;
Word_Size    : constant := 32;

Storage_Unit is the number of bits per memory storage element. Storage elements are the components of memory cells, and typically correspond to the individually addressable memory elements. A "byte" would correspond to a storage element with the above constant value.

Consider a typical idiom for determining the number of whole storage elements an object named X occupies:

Units : constant Integer := (X'Size + Storage_Unit - 1) / Storage_Unit;

Remember that 'Size returns a value in terms of bits. There are more direct ways to determine that size information but this will serve as an example of the sort of thing you might do with that constant.

A machine "word" is the largest amount of storage that can be conveniently and efficiently manipulated by the hardware, given the implementation's run-time model. A word consists of some number of storage elements, maybe one but typically more than one. As the unit the machine natively manipulates, words are expected to be independently addressable. (On some machines only words are independently addressable.)

Word_Size is the number of bits in the machine word. On a 32-bit machine we'd expect Word_Size to have a value of 32; on a 64-bit machine it would probably be 64, and so on.

Storage_Unit and Word_Size are obviously related.

Another frequently referenced declaration in package System is that of the type representing memory addresses, along with a constant for the null address designating no storage element.

type Address is private;
Null_Address : constant Address;

You may be wondering why type Address is a private type, since that choice means that we programmers cannot treat it like an ordinary (unsigned) integer value. Portability is of course the issue, because addressing, and thus address representation, varies among computer architectures. Not all architectures have a flat address space directly referenced by numeric values, although that is common. Some are represented by a base address plus an offset, for example. Therefore, the representation for type Address is hidden from us, the clients. Consequently we cannot simply treat address values as numeric values. Don't worry, though. The operations we need are provided.

Package System declares these comparison functions, for example:

function "<"  (Left, Right : Address) return Boolean;
function "<=" (Left, Right : Address) return Boolean;
function ">"  (Left, Right : Address) return Boolean;
function ">=" (Left, Right : Address) return Boolean;
function "="  (Left, Right : Address) return Boolean;

These functions are intrinsic, i.e., built-in, meaning that the compiler generates the code for them directly at the point of calls. There is no actual function body for any of them so there is no performance penalty.

Any private type directly supports the equality function, and consequently the inequality function, as well as assignment. What we don't get here is address arithmetic, again because we don't have a compile-time view of the actual representation. That functionality is provided by package System.Storage_Elements, a child package we will cover later. We should say though, that the need for address arithmetic in Ada is rare, especially compared to C.

Having type Address presented as a private type is not, strictly speaking, required by the language. Doing so is a good idea for the reasons given above, and is common among vendors. Not all vendors do, though.

Note that Address is the type of the result of the query attribute Address.

We mentioned potentially needing to swap bytes in networking communications software, due to the differences in the "endianness" of the machines communicating. That characteristic can be determined via a constant declared in package System as follows:

type Bit_Order is (High_Order_First, Low_Order_First);
Default_Bit_Order : constant Bit_Order := implementation-defined;

High_Order_First corresponds to "Big Endian" and Low_Order_First to "Little Endian." On a Big Endian machine, bit 0 is the most significant bit. On a Little Endian machine, bit 0 is the least significant bit.

Strictly speaking, this constant gives us the default order for bits within storage elements in record representation clauses, not the order of bytes within words. However, we can usually use it for the byte order too. In particular, if Word_Size is greater than Storage_Unit, a word necessarily consists of multiple storage elements, so the default bit ordering is the same as the ordering of storage elements in a word.

Let's take that example of swapping the bytes in a received Ethernet packet. The "wire" format is Big Endian so if we are running on a Little Endian machine we must swap the bytes received.

Suppose we want to retrieve typed values from a given buffer or bytes. We get the bytes from the buffer into a variable named Value, of the type of interest, and then swap those bytes within Value if necessary.

   ...
begin
   Value := ...

   if Default_Bit_Order /= High_Order_First then
      -- we're not on a Big Endian machine
      Value := Byte_Swapped (Value);
   end if;
end Retrieve_4_Bytes;

We have elided the code that gets the bytes into Value, for the sake of simplicity. How the bytes are actually swapped by function Byte_Swapped is also irrelevant. The point here is the if-statement: the expression compares the Default_Bit_Order constant to High_Order_First to see if this execution is on a Big Endian machine. If not, it swaps the bytes because the incoming bytes are always received in "wire-order," i.e., Big Endian order.

Another important set of declarations in package System define the values for priorities, including interrupt priorities. We will ignore them until we get to the section on interrupt handling.

Finally, and perhaps surprisingly, a few declarations in package System are almost always (if not actually always) ignored.

type Name is implementation-defined-enumeration-type;
System_Name : constant Name := implementation-defined;

Values of type Name are the names of alternative machine configurations supported by the implementation. System_Name represents the current machine configuration. We've never seen any actual use of this.

Memory_Size is an implementation-defined value that is intended to reflect the memory size of the configuration, in units of storage elements. What the value actually refers to is not specified. Is it the size of the address space, i.e., the amount possible, or is it the amount of physical memory actually on the machine, or what? In any case, the amount of memory available to a given computer is neither dependent upon, nor reflected by, this constant. Consequently, Memory_Size is not useful either.

Why have something defined in the language that nobody uses? In short, it seemed like a good idea at the time when Ada was first defined. Upward-compatibility concerns propagate these declarations forward as the language evolves, just in case somebody does use them.

Querying Representation Choices

As we mentioned in the introduction, in low-level programming the hardware and the compiler's representation choices can come to the forefront. You can, therefore, query many such choices.

For example, let's say we want to query the addresses of some objects because we are calling the imported C memcpy function. That function requires two addresses to be passed to the call: one for the source, and one for the destination. We can use the 'Address attribute to get those values.

We will explore importing routines and objects implemented in other languages elsewhere. For now, just understand that we will have an Ada declaration for the imported routine that tells the compiler how it should be called. Let's assume we have an Ada function declared like so:

function MemCopy
  (Destination : System.Address;
   Source      : System.Address;
   Length      : Natural)
return Address
with
  Import,
  Convention => C,
  Link_Name => "memcpy",
  Pre  => Source /= Null_Address      and then
          Destination /= Null_Address and then
          not Overlapping (Destination, Source, Length),
  Post => MemCopy'Result = Destination;
--  Copies Length bytes from the object designated by Source to the object
--  designated by Destination.

The three aspects that do the importing are specified after the reserved word with but can be ignored for this discussion. We'll talk about them later. The preconditions make explicit the otherwise implicit requirements for the arguments passed to memcpy, and the postcondition specifies the expected result returned from a successful call. Neither the preconditions nor the postconditions are required for importing external entities but they are good "guard-rails" for using those entities. If we call it incorrectly the precondition will inform us, and likewise, if we misunderstand the result the postcondition will let us know (at least to the extent that the return value does that).

For a sample call to our imported routine, imagine that we have a procedure that copies the bytes of a String parameter into a Buffer parameter, which is just a contiguous array of bytes. We need to tell MemCopy the addresses of the arguments passed so we apply the 'Address attribute accordingly:

procedure Put (This : in out Buffer; Start : Index; Value : String) is
   Result : System.Address with Unreferenced;
begin
   Result := MemCopy (Destination => This (Start)'Address,
                      Source      => Value'Address,
                      Length      => Value'Length);
end Put;

The order of the address parameters is easily confused so we use the named association format for specifying the actual parameters in the call.

Although we assign Result we don't otherwise use it, so we tell the compiler this is not a mistake via the Unreferenced aspect. And if we do turn around and reference it the compiler will complain, as it should. Note that Unreferenced is defined by GNAT, so usage is not necessarily portable. Other vendors may or may not implement something like it, perhaps with a different name.

(We don't show the preconditions for Put, but they would have specified that Start must be a valid index into this particular buffer, and that there must be room in the Buffer argument for the number of bytes in Value when starting at the Start index, so that we don't copy past the end of the Buffer argument.)

There are other characteristics we might want to query too.

We might want to ask the compiler what alignment it chose for a given object (or type, for all such objects).

For a type, when Alignment returns a non-zero value we can be sure that the compiler will allocate storage for objects of the type at correspondingly aligned addresses (unless we force it to do otherwise). Similarly, references to dynamically allocated objects of the type will be to properly aligned locations. Otherwise, an Alignment of zero means that the guarantee does not hold. That could happen if the type is packed down into a composite object, such as an array of Booleans. We'll discuss "packing" soon. More commonly, the smallest likely value is 1, meaning that any storage element's address will suffice. If the machine has no particular natural alignments, then all type alignments will probably be 1 by default. That would be somewhat rare today, though, because modern processors usually have comparatively strict alignment requirements.

We can ask for the amount of storage associated with various entities. For example, when applied to a task, 'Storage_Size tells us the number of storage elements reserved for the task's execution. The value includes the size of the task's stack, if it has one. We aren't told if other required storage, used internally in the implementation, is also included in this number. Often that other storage is not included in this number, but it could be.

Storage_Size is also defined for access types. The meaning is a little complicated. Access types can be classified into those that designate only variables and constants ("access-to-object") and those that can designate subprograms. Each access-to-object type has an associated storage pool. The storage allocated by new comes from the pool, and instances of Unchecked_Deallocation return storage to the pool.

When applied to an access-to-object type, Storage_Size gives us the number of storage elements reserved for the corresponding pool.

Note that Storage_Size doesn't tell us how much available, unallocated space remains in a pool. It includes both allocated and unallocated space. Note, too, that although each access-to-object type has an associated pool, that doesn't mean that each one has a distinct, dedicated pool. They might all share one, by default. On an operating system, such as Linux, the default shared pool might even be implicit, consisting merely of calls to the OS routines in C.

As a result, querying Storage_Size for access types and tasks is not necessarily all that useful. Specifying the sizes, on the other hand, definitely can be useful.

That said, we can create our own pool types and define precisely how they are sized and how allocation and deallocation work, so in that case querying the size for access types could be more useful.

For an array type or object, 'Component_Size provides the size in bits of the individual components.

More useful are the following two attributes that query a degree of memory sharing between objects.

Applied to an object, 'Has_Same_Storage is a Boolean function that takes another object of any type as the argument. It indicates whether the two objects' representations occupy exactly the same bits.

Applied to an object, 'Overlaps_Storage is a Boolean function that takes another object of any type as the argument. It indicates whether the two objects' representations share at least one bit.

Generally, though, we specify representation characteristics far more often than we query them. Rather than describe all the possibilities, we can just say that all the representation characteristics that can be specified can also be queried. We cover specifying representation characteristics next, so just assume the corresponding queries are available.

That said, there is one particular representation query we need to talk about explicitly, now, because there is a lot of confusion about it: the 'Size attribute. The confusion stems from the fact that there are multiple contexts for applying the attribute, and multiple reasonable interpretations possible. We can apply the 'Size attribute to a type, in an attempt to get information about all objects of the type, or we can apply it to individual objects to get specific information. In both cases, what actual information do we get? In the original version of Ada these questions weren't really answered so vendors did what they thought was correct. But they did not agree with each other, and portability became a problem.

For example, suppose you want to convert some value to a series of bytes in order to send the value over the wire. To do that you need to know how many bytes are required to represent the value. Many applications queried the size of the type to determine that, and then, when porting to a new vendor's compiler, found that their code no longer worked correctly. The new vendor's implementation wasn't wrong, it was just different.

Later versions of Ada answered these questions, where possible, so let's examine the contexts and meaning. Above all, though, remember that 'Size returns values in terms of bits.

If we apply 'Size to a type, the resulting value depends on the kind of type.

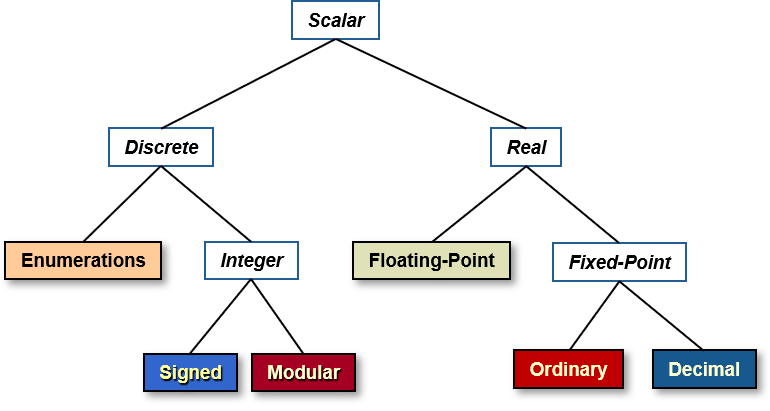
For scalar types, the attribute returns the minimum number of bits required to represent all the values of the type. Here's a diagram showing what the category "scalar types" includes:

Consider type Boolean, which has two possible values. One bit will suffice, and indeed the language standard requires Boolean'Size to be the value 1.

This meaning also applies to subtypes, which can constrain the number of values for a scalar type. Consider subtype Natural. That's a subtype defined by the language to be type Integer but with a range of 0 .. Integer'Last. On a 32-bit machine we would expect Integer to be a native type, and thus 32-bits. On such a machine if we say Integer'Size we will indeed get 32. But if we say Natural'Size we will get 31, not 32, because only 31 bits are needed to represent that range on that machine.

The size of objects, on the other hand, cannot be just a matter of the possible values. Consider type Boolean again, where Boolean'Size is required to be 1. No compiler is likely to allocate one bit to a Boolean variable, because typical machines don't support individually-addressable bits. Instead, addresses refer to storage elements, of a size indicated by the Storage_Unit constant. The compiler will allocate the smallest number of storage elements necessary, consistent with other considerations such as alignment. Therefore, for a machine that has Storage_Unit set to a value of eight, we can assume that a compiler for that machine will allocate an entire eight-bit storage element to a stand-alone Boolean variable. The other seven bits are simply not used by that variable. Moreover, those seven bits are not used by any other stand-alone object either, because access would be far less efficient, and such sharing would require some kind of locking to prevent tasks from interfering with each other when accessing those stand-alone objects. (Stand-alone objects are independently addressable; they wouldn't stand alone otherwise.)

By the same token (and still assuming a 32-bit machine), a compiler will allocate more than 31 bits to a variable of subtype Natural because there is no 31-bit addressable unit. The variable will get all 32-bits.

Note that we're talking about individual, stand-alone variables. Components of composite types, on the other hand, might indeed share bytes if the individual components don't require all the bits of their storage elements. You'd have to request that representation, though, with most implementations, because accessing the components at run-time would require more machine instructions. We'll go into the details of that later.

Let's talk further about sizes of types.

For record types, 'Size gives the minimum number of bits required to represent the whole composite value. But again, that's not necessarily the number of bits required for the objects' in-memory representation. The order of the components within the record can make a difference, as well as their alignments. The compiler will respect the alignment requirements of the components, and may add padding bytes within the record and also at the end to ensure components start at addresses compatible with their alignment requirements. As a result the overall size could be larger.

Note that Ada compilers are allowed to reorder the components; the order in memory might not match the order in the source code.

For example, consider this record type and its components:

In the figure, we see a record type with some components, and a sample layout for that record type assuming the compiler does not reorder the components. Observe that some bytes allocated to objects of type R are unused (the darkly shaded ones). In this case that's because the alignment of subtype S happens to be 4 on this machine. The component X of that subtype S cannot start at byte offset 1, or 2, or 3, because those addresses would not satisfy the alignment constraint of S. (We're assuming byte 0 is at a word-aligned address.) Therefore, X starts at the object's starting address plus 4. Components B and C are of types that have an alignment of 1, so they can start at any storage element. They immediately follow the bytes allocated to component X. Therefore, R'Size is 80, or 10 bytes. The three bytes following component M are simply not used.

But what about the two bytes following the last component C? They could be allocated to stand-alone objects if they would fit. More likely, though, the compiler will allocate those two bytes to objects of type R, that is, 12 bytes instead of 10 are allocated. As a result, 96 bits are actually used in memory. The extra, unused 16 bits are "padding."

Why add unused padding? It simplifies the memory allocation of objects of type R. Suppose some array type has components of record type R. Assuming the first component is aligned properly, every following component will also be aligned properly, automatically, because the two padding bytes are considered parts of the components.

To make that work, the compiler takes the most stringent alignment of all the record type's components and uses that for the alignment of the overall record type. That way, any address that satisfies the record object's alignment will satisfy the components' alignment requirements. The alignment is component X, of subtype S, is 4. The other components have an alignment of 1, therefore R'Alignment is 4. An aligned address plus 12 will also be an aligned address.

This rounding up based on alignment is recommended behavior for the compiler, not a requirement, but is reasonable and typical among vendors. Although it can result in unused storage, that's the price paid for speed of access (or even correctness for machines that would fault on misaligned component accesses).

As you can see, alignment is a critical factor in the sizes of composite objects. If you care about the layout of the type you very likely need to care about the alignment of the components and overall record type.

Ada compilers are allowed to reorder the components of record types in order to minimize these gaps or satisfy the alignment requirements of the components. Some compilers do, some don't. Consider the type R again, this time with the first two components switched in the component declaration order:

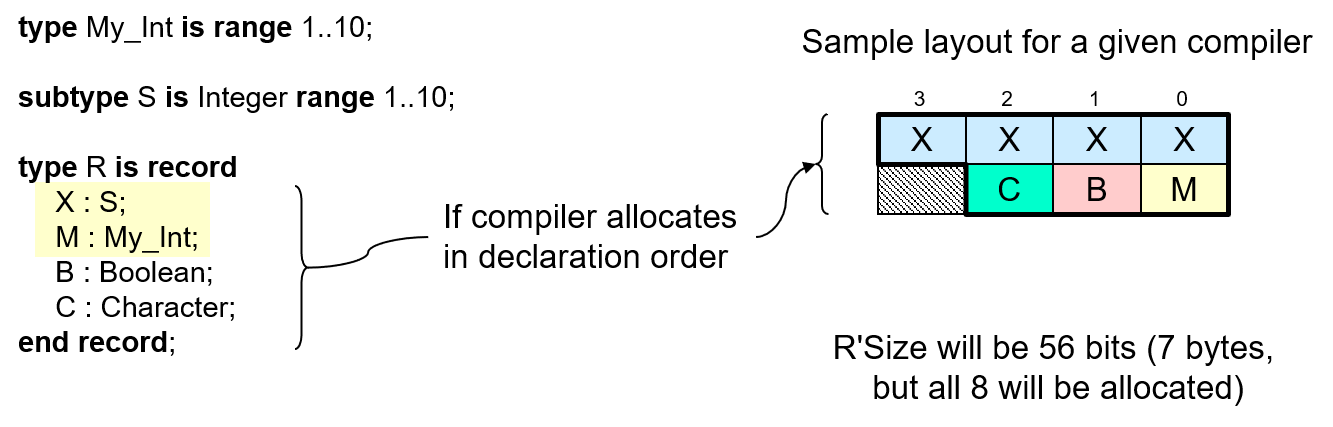
Now R'Size will report 56 bits instead of 80. The one trailing byte will still be padding, but only that one.

What about unbounded types, for example type String? Querying the 'Size in that case would provide an implementation-defined result. A somewhat silly thing to do, really, since the type — by definition — doesn't specify how many components are involved.

Usually, though, you don't want to query the size of a type. Most of the time what you want is the size of objects of the type. Going back to sending values over the wire, the code should query the size of the parameter holding the value to be sent. That will tell you how many bits are really needed.

One last point: GNAT, and now Ada 202x, define an attribute named Object_Size. It does just what the name suggests: what 'Size does when applied to objects rather than types. GNAT also defines another attribute, named Value_Size, that does what 'Size does when applied to types. The former is far more useful so Ada has standardized it.

Specifying Representation

Recall that we said Boolean'Size is required to be 1, and that stand-alone objects of type Boolean are very likely allocated some integral number of storage elements (e.g., bytes) in memory, typically one. What about arrays of Booleans? Suppose we have an array of 16 Boolean components. How big are objects of the array type? It depends on the machine. Continuing with our hypothetical (but typical) byte-addressable machine, for the sake of efficient access each component is almost certainly allocated an individual byte rather than a single bit, just like stand-alone objects. Consequently, our array of 16 Booleans will be reported by 'Size to be 128 bits, i.e., 16 bytes. If you wanted a bit-mask, in which each Boolean component is allocated a single bit and the total array size is 16 bits, you'd have a problem. The compiler assumes you want speed of access rather than storage minimization, and normally that would be the right assumption.

Naturally there is a solution. Ada allows us to specify the representation characteristics of types, and thus objects of those types, including their bit-wise layouts. It also allows us to specify the representation of individual objects. You should understand, though, that the compiler is not required to do what you ask, because you might ask the impossible. For example, if you specify that the array of 16 Booleans is to be represented completely in 15 bits, what can the compiler do? Rejecting that specification is the only reasonable response. But if you specify something possible, the compiler must do what you ask, absent some compelling reason to the contrary.

With that in mind, let's examine setting the size for types.

So, how do we specify that we want our array of 16 Boolean components to be allocated one bit per component, for a total allocation of 16 bits? There are a couple of ways, one somewhat better than the other.

First, you can ask that the compiler "pack" the components into as small a number of bits as it can:

type Bits16 is array (0 .. 15) of Boolean with
  Pack;

That likely does what you want: Bits16'Size will probably be 16.

But realize that the Pack aspect (and corresponding pragma) is merely a request that the compiler do its best to minimize the number of bits allocated, not necessarily that it do exactly what you expected or required.

We could set the size of the entire array type:

type Bits16 is array (0 .. 15) of Boolean with
  Size => 16;

But the language standard says that a Size clause on array and record types should not affect the internal layout of their components. That's Implementation Advice, so not normative, but implementations are really expected to follow the advice, absent some compelling reason. That's what the Pack aspect, record representation clauses, and Component_Size clauses are for. (We'll talk about record representation clauses momentarily.) That said, at least one other vendor's compiler would have changed the size of the array type because of the Size clause, so GNAT defines a configuration pragma named Implicit_Packing that overrides the default behavior. With that pragma applied, the Size clause would compile and suffice to make the overall size be 16. That's a vendor-defined pragma though, so not portable.

Therefore, the best way to set the size for the array type is to set the size of the individual components, via the Component_Size aspect as the Implementation Advice indicates. That will say what we really want, rather than a "best effort" request for the compiler, and is portable:

type Bits16 is array (0 .. 15) of Boolean with
  Component_Size => 1;

With this approach the compiler must either use the specified size for each component or refuse to compile the code. If it compiles, objects of the array type will be 16 bits total (plus any padding bits required to make objects have a size that is a multiple of Storage_Unit, typically zero on modern machines).

Now that we have a bit-mask array type, let's put it to use.

Let's say that you have an object that is represented as a simple signed integer because, for most usage, that's the appropriate representation. Sometimes, though, let's say you need to access individual bits of the object instead of the whole numeric value. Signed integer types don't provide bit-level access. In Ada we'd say that the "view" presented by the object's type doesn't include bit-oriented operations. Therefore, we need to add a view to the object that does provide them. A different view will require an additional type for the same object.

Applying different types, and thus their operations, to the same object is known as type punning in computer programming. Realize that doing so circumvents the static strong typing we harness to protect us from ourselves and from others. Use it with care! (For example, limit the compile-time visibility to such code.)

One way to add a view is to express an "overlay," in which an object of one type is placed at the same memory location as a distinct object of a different type, thus "overlaying" one object over the other in memory. The different types present different views, therefore different operations available for the shared memory cells. Our hypothetical example uses two views, but you can overlay as many different views as needed. (That said, requiring a large number of different views of the same object would be suspect.)

There are other ways in Ada to apply different views, some more flexible than others, but an overlay is a simple one that will often suffice.

Here is an implementation of the overlay approach, using our bit-mask array type:

type Bits32 is array (0 .. 31) of Boolean with
  Component_Size => 1;

X : Integer;
Y : Bits32 with Address => X'Address;

We can query the addresses of objects, and other things too, but objects, especially variables, are the most common case. In the above, we say X'Address to query the starting address of object X. With that information we know what address to specify for our bit-mask overlay object Y. Now X and Y are aliases for the same memory cells, and therefore we can manipulate and query that memory as either a signed integer or as an array of bits. Reading or updating individual array components accesses the individual bits of the overlaid object.

Instead of the Bits32 array type, we could have specified a modular type for the overlay Y to get a view providing bit-oriented operations. Overlaying such an array was a common idiom prior to the introduction of modular "unsigned" types in Ada, and remains useful for accessing individual bits. In other words, using a modular type for Y, you could indeed access an individual bit by passing a mask value to the and operator defined in any modular type's view. Using a bit array representation lets the compiler do that work for you, in the generated code. The source code will be both easier to read and more explicit about what it is doing when using the bit array overlay.

One final issue remains: in our specific overlay example the compiler would likely generate code that works. But strictly speaking it might not.

The Ada language rules say that for such an overlaid object — Y in the example above — the compiler should not perform optimizations regarding Y that it would otherwise apply in the absence of aliases. That's necessary, functionally, but may imply degraded performance regarding Y, so keep it in mind. Aliasing precludes some desirable optimizations.

But what about X in the example above? We're querying that object's address, not specifying it, so the RM rule precluding optimizations doesn't apply to X. That can be problematic.

The compiler might very well place X in a register, for example, for the sake of the significant performance increase (another way of being friendly). But in that case System.Null_Address will be returned by the X'Address query and, consequently, the declaration for Y will not result in the desired overlaying.

Therefore, we should mark X as explicitly aliased to ensure that X'Address is well-defined:

type Bits32 is array (0 .. 31) of Boolean with
  Component_Size => 1;

X : aliased Integer;
Y : Bits32 with Address => X'Address;

The only difference in the version above is the addition of aliased in the declaration of X. Now we can be certain that the optimizer will not represent X in some way incompatible with the idiom, and X'Address will be well-defined.

In our example X and Y are clearly declared in the same compilation unit. Most compilers will be friendly in this scenario, representing X in such a way that querying the address will return a non-null address value even if aliased is not applied. Indeed, aliased is relatively new to Ada, and earlier compilers typically emitted code that would handle the overlay as intended.

But suppose, instead of being declared in the same declarative part, that X was declared in some other compilation unit. Let's say it is in the visible part of a package declaration. (Assume X is visible to clients for some good reason.) That package declaration can be, and usually will be, compiled independently of clients, with the result that X might be represented in some way that cannot supporting querying the address meaningfully.

Therefore, the declaration of X in the package spec should be marked as aliased, explicitly:

package P is
   X : aliased Integer;
end P;

Then, in the client code declaring the overlay, we only declare Y, assuming a with-clause for P:

type Bits32 is array (0 .. 31) of Boolean with
  Component_Size => 1;

Y : Bits32 with Address => P.X'Address;

All well and good, but how did the developer of the package know that some other unit, a client of the package, would query the address of X, such that it needed to be marked as aliased? Indeed, the package developer might not know. Yet the programmer is responsible for ensuring a valid and appropriate Address value is used in the declaration of Y. Execution is erroneous otherwise, so we can't say what would happen in that case. Maybe an exception is raised or a machine trap, maybe not.

Worse, the switches that were applied when compiling the spec for package P can make a difference: P.X might not be placed in a register unless the optimizer is enabled. Hence the client code using Y might work as expected when built for debugging, with the optimizer disabled, and then not do so when re-built for the final release. You'd probably have to solve this issue by debugging the application.

On a related note, you may be asking yourself how to know that type Integer is 32 bits wide, so that we know what size array to use for the bit-mask. The answer is that you just have to know the target well when doing low-level programming. The hardware becomes much more visible, as we mentioned.

That said, you could at least verify the assumption:

pragma Compile_Time_Error (Integer'Object_Size /= 32,
                           "Integers expected to be 32 bits");
X : aliased Integer;
Y : Bits32 with Address => X'Address;

That's a vendor-defined pragma so this is not fully portable. It isn't an unusual pragma, though, so at least you can probably get the same functionality even if the pragma name varies.

Overlays aren't always structured like our example above, i.e., with two objects declared at the same time. We might apply a different type to the same memory locations at different times. Here's an example from the ADL to illustrate the idea. We'll elaborate on this example later, in another section.

First, a package declaration, with two functions that provide a device-specific unique identifier located in shared memory. Each function provides the same Id value in a distinct format. One format is a string of 12 characters, the other is a sequence of three 32-bit values. Hence both representations are the same size.

package STM32.Device_Id is

   subtype Device_Id_Image is String (1 .. 12);

   function Unique_Id return Device_Id_Image;

   type Device_Id_Tuple is array (1 .. 3) of UInt32
     with Component_Size => 32;

   function Unique_Id return Device_Id_Tuple;

end STM32.Device_Id;

In the package body we implement the functions as two ways to access the same shared memory, specified by ID_Address:

with System;

package body STM32.Device_Id is

   ID_Address : constant System.Address := System'To_Address (16#1FFF_7A10#);

   function Unique_Id return Device_Id_Image is
      Result : Device_Id_Image with Address => ID_Address, Import;
   begin
      return Result;
   end Unique_Id;

   function Unique_Id return Device_Id_Tuple is
      Result : Device_Id_Tuple with Address => ID_Address, Import;
   begin
      return Result;
   end Unique_Id;

end STM32.Device_Id;

System'To_Address is just a convenient way to convert a numeric value into an Address value. The primary benefit is that the call is a static expression, but we can ignore that here. Using Import is a good idea to ensure that the Ada code does no initialization of the object, since the value is coming from the hardware via the shared memory. Doing so may not be necessary, depending on the type used, but is a good habit to develop.

The point of this example is that we have one object declaration per function, of a type corresponding to the intended function result type. Because each function places their local object at the same address, they are still overlaying the shared memory.

Now let's return, momentarily, to setting the size of entities, but now let's focus on setting the size of objects.

We've said that the size of an object is not necessarily the same as the size of the object's type. The object size won't be smaller, but it could be larger. Why? For a stand-alone object or a parameter, most implementations will round the size up to a storage element boundary, or more, so the object size might be greater than that of the type. Think back to Boolean, where Size is required to be 1, but stand-alone objects are probably allocated 8 bits, i.e., an entire storage element (on our hypothetical byte-addressed machine).

Likewise, recall that numeric type declarations are mapped to underlying hardware numeric types. These underlying numeric types provide at least the capabilities we request with our type declarations, e.g., the range or number of digits, perhaps more. But the mapped numeric hardware type cannot provide less than requested. If there is no underlying hardware type with at least our requested capabilities, our declarations won't compile. That mapping means that specifying the size of a numeric type doesn't necessarily affect the size of objects of the type. That numeric hardware type is the size that it is, and is fixed by the hardware.

For example, let's say we have this declaration:

type Device_Register is range 0 .. 2**5 - 1 with Size => 5;

That will compile successfully, because there will be a signed integer hardware type with at least that range. (Not necessarily, legally speaking, but realistically speaking, there will be such a hardware type.) Indeed, it may be an 8-bit signed integer, in which case Device_Register'Size will give us 5, but objects of the type will have a size of 8, unavoidably, even though we set Size to 5.

The difference between the type and object sizes can lead to potentially problematic code:

type Device_Register is range 0 .. 2**8 - 1 with Size => 8;

My_Device : Device_Register
  with Address => To_Address (...);

The code compiles successfully, and tries to map a byte to a hardware device that is physically connected to one storage element in the processor memory space. The actual address is elided as it is not important here.

That code might work too, but it might not. We might think that My_Device'Size is 8, and that My_Device'Address points at an 8-bit location. However, this isn't necessarily so, as we saw with the supposedly 5-bit example earlier. Maybe the smallest signed integer the hardware has is 16-bits wide. The code would compile because a 16-bit signed numeric type can certainly handle the 8-bit range requested. My_Device'Size would be then 16, and because 'Address gives us the starting storage element, My_Device'Address might designate the high-order byte of the overall 16-bit object. When the compiler reads the two bytes for My_Device what will happen? One of the bytes will be the data presented by the hardware device mapped to the memory. The other byte will contain undefined junk, whatever happens to be in the memory cell at the time. We might have to debug the code a long time to identify that as the problem. More likely we'll conclude we have a failed device.

The correct way to write the code is to specify the size of the object instead of the type:

type Device_Register is range 0 .. 2**8 - 1;

My_Device : Device_Register with
  Size => 8,
  Address => To_Address (...);

If the compiler cannot support stand-alone 8-bit objects for the type, the code won't compile.

Alternatively, we could change the earlier Size clause on the type to apply Object_Size instead:

type Device_Register is range 0 .. 2**8 - 1 with Object_Size => 8;

My_Device : Device_Register with
  Address => To_Address (...);

The choice between the two approaches comes down to personal preference, at least if only a small number of stand-alone objects of the type are going to be declared. With either approach, if the implementation cannot support 8-bit stand-alone objects, we find out that there is a problem at compile-time. That's always cheaper than debugging.

You might conclude that setting the Size for a type serves no purpose. That's not an unreasonable conclusion, given what you've seen, but in fact there are reasons to do so. However, there are only a few specific cases so we will save the reasons for the discussions of the specific cases.

There is one general case, though, for setting the 'Size of a type. Specifically, you may want to specify the size that you think is the minimum possible, and you want the compiler to confirm that belief. This would be one of the so-called "confirming" representation clauses, in which the representation detail is what the compiler would have chosen anyway, absent the specification. You're not actually changing anything, you're just getting confirmation via Size whether or not the compiler accepts the clause. Suppose, for example, that you have an enumeration type with 256 values. For enumeration types, the compiler allocates the smallest number of bits required to represent all the values, rounded up to the nearest storage element. (It's not like C, where enums are just named int values.) For 256 values, an eight-bit byte would suffice, so setting the size to 8 would be confirming. But suppose we actually had 257 enumerals, accidentally? Our size clause set to 8 would not compile, and we'd be told that something is amiss.

However, note that if your supposedly "confirming" size clause actually specifies a size larger than what the compiler would have chosen, you won't know, because the compiler will silently accept sizes larger than necessary. It just won't accept sizes that are too small.

There are other confirming representation clauses as well. Thinking again of enumeration types, the underlying numeric values are integers, starting with zero and consecutively increasing from there up to N-1, where N is the total number of enumeral values.

For example:

type Commands is (Off, On);

for Commands use (Off => 0, On => 1);

As a result, Off is encoded as 0 and On as 1. That specific underlying encoding is guaranteed by the language, as of Ada 95, so this is just a confirming representation clause nowadays. But it was not guaranteed in the original version of the language, so if you wanted to be sure of the encoding values you would have specified the above. It wasn't necessarily confirming before Ada 95, in other words.

But let's also say that the underlying numeric values are not what you want because you're interacting with some device and the commands are encoded with values other than 0 and 1. Maybe you want to use an enumeration type because you want to specify all the possible values actually used by clients. If you just used some numeric type instead and made up constants for On and Off, there's nothing to keep clients from using other numeric values in place of the two constants (absent some comparatively heavy code to prevent that from happening). Better to use the compiler to make that impossible in the first place, rather than debug the code to find the incorrect values used. Therefore, we could specify different encodings:

for Commands use (Off => 2, On => 4);

Now the compiler will use those encoding values instead of 0 and 1, transparently to client code.

The encoding values specified must maintain the relative ordering, otherwise the relational operators won't work correctly. For example, for type Commands above, Off is less than On, so the specified encoding value for Off must be less than that of On.

Note that the values given in the example no longer increase consecutively, i.e., there's a gap. That gap is OK, in itself. As long as we use the two enumerals the same way we'd use named constants, all is well. Otherwise, there is both a storage issue and a performance issue possible. Let's say that we use that enumeration type as the index for an array type. Perfectly legal, but how much storage is allocated to objects of this array type? Enough for exactly two components? Four, with two unused? The answer depends on the compiler, and is therefore not portable. The bigger the gaps, the bigger the overall storage difference possible. Likewise, imagine we have a for-loop iterating over the index values of one of these array objects. The for-loop parameter cannot be coded by the compiler to start at 0, clearly, because there is no index (enumeration) value corresponding to 0. Similarly, to get the next index, the compiler cannot have the code simply increment the current value. Working around that takes some extra code, and takes some extra time that would not be required if we did not have the gaps.

The performance degradation can be significant compared to the usual code generated for a for-loop. Some coding guidelines say that you shouldn't use an enumeration representation clause for this reason, with or without gaps. Now that Ada has type predicates we could limit the values used by clients for a numeric type, so an enumeration type is not the only way to get a restricted set of named, encoded values.

type Commands is new Integer with
   Static_Predicate => Commands in 2 | 4;

On    : constant Commands := 2;
Off   : constant Commands := 4;

The storage and performance issues bring us back to confirming clauses. We want the compiler to recognize them as such, so that it can generate the usual code, thereby avoiding the unnecessary portability and performance issues. Why would we have such a confirming clause now? It might be left over from the original version of the language, written before the Ada 95 change. Some projects have lifetimes of several decades, after all, and changing the code can be expensive (certified code, for example). Whether the compiler does recognize confirming clauses is a feature of the compiler implementation. We can expect a mature compiler to do so, but there's no guarantee.

Now let's turn to what is arguably the most common representation specification, that of record type layouts.

Recall from the discussion above that Ada compilers are allowed to reorder record components in physical memory. In other words, the textual order in the source code is not necessarily the physical order in memory. That's different from, say, C, where what you write is what you get, and you better know what you're doing. On some targets a misaligned struct component access will perform very poorly, or even trap and halt, but that's not the C compiler's fault. In Ada you'd have to explicitly specify the problematic layout. Otherwise, if compilation is successful, the Ada compiler must find a representation that will work, either by reordering the components or by some other means. Otherwise it won't compile.

GNAT did not reorder components until relatively recently but does now, at least for the more egregious performance cases. It does this reordering silently, too, although there is a switch to have it warn you when it does. To prevent reordering, GNAT defines a pragma named No_Component_Reorder that does what the name suggests. You can apply it to individual record types, or globally, as a configuration pragma. But of course because the pragma is vendor defined it is not portable.

Therefore, if you care about the record components' layout in memory, the best approach is to specify the layout explicitly. For example, perhaps you are passing data to code written in C. In that case, you need the component order in memory to match the order given in the corresponding C struct declaration. That order in memory is not necessarily guaranteed from the order in the Ada source code. The Ada compiler is allowed to chose the representation unless you specify it, and it might chose a different layout from the one given. (Ordinarily, letting the compiler chose the layout is the most desirable approach, but in this case we have an external layout requirement.)

Fortunately, specifying a record type's layout is straightforward. The record layout specification consists of the storage places for some or all components, specified with a record representation clause. This clause specifies the order, position, and size of components (including discriminants, if any).

The approach is to first define the record type, as usual, using any component order you like — you're about to specify the physical layout explicitly, in the next step.

Let's reuse that record type from the earlier discussion:

type My_Int is range 1 .. 10;

subtype S is Integer range 1 .. 10;

type R is record
   M : My_Int;
   X : S;
   B : Boolean;
   C : Character;
end record;

The resulting layout might be like so, assuming the compiler doesn't reorder the components:

As a result, R'Size will be 80 bits (10 bytes), but those last two bytes will be will be allocated to objects, for an Object_Size of 96 bits (12 bytes). We'll change that with an explicit layout specification.

Having declared the record type, the second step consists of defining the corresponding record representation clause giving the components' layout. The clause uses syntax that somewhat mirrors that of a record type declaration. The components' names appear, as in a record type declaration. But now, we don't repeat the components' types, instead we give their relative positions within the record, in terms of a relative offset that starts at zero. We also specify the bits we want them to occupy within the storage elements starting at that offset.

for R use record
   X at 0 range 0 .. 31;  -- note the order swap,
   M at 4 range 0 ..  7;  -- with this component
   B at 5 range 0 ..  7;
   C at 6 range 0 ..  7;
end record;

Now we'll get the optimized order, and we'll always get that order, or the layout specification won't compile in the first place. In the following diagram, both layouts, the default, and the one resulting from the record representation clause, are depicted for comparison:

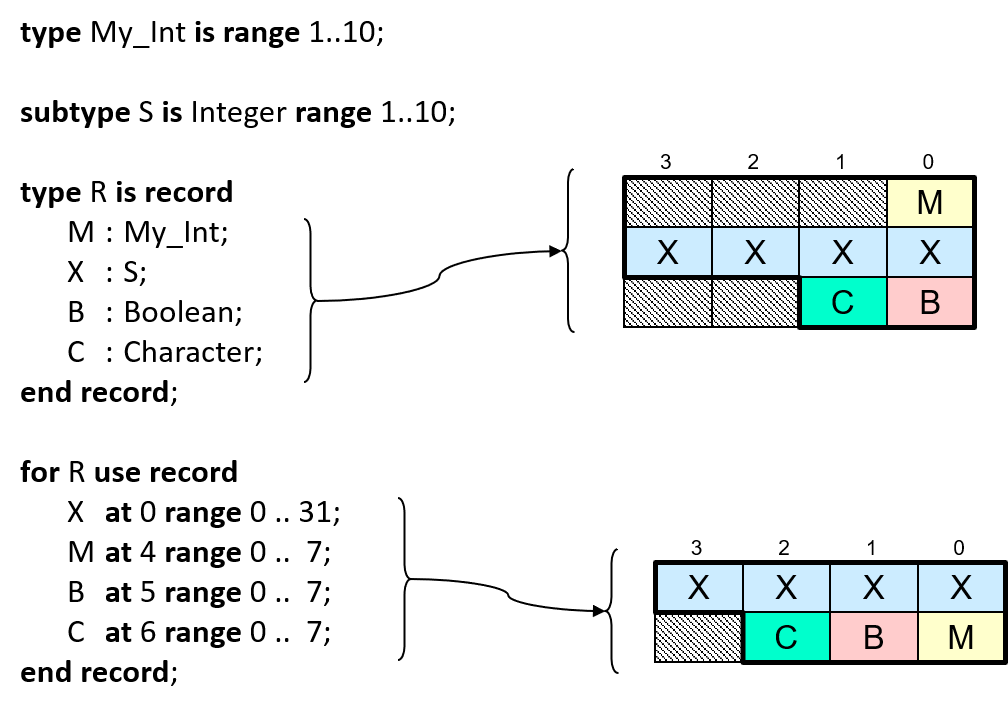
R'Size will be 56 bits (7 bytes), but that last padding byte will also be allocated to objects, so the Object_Size will be 64 bits (8 bytes).

Notice how we gave each component an offset, after the reserved word at. These offsets are in terms of storage elements, and specify their positions within the record object as a whole. They are relative to the beginning of the memory allocated to the record object so they are numbered starting at zero. We want the X component to be the very first component in the allocated memory so the offset for that one is zero. The M component, in comparison, starts at an offset of 4 because we are allocating 4 bytes to the prior component X: bytes 0 through 3 specifically. M just occupies one storage element so the next component, B, starts at offset 5. Likewise, component C starts at offset 6.

Note that there is no requirement for the components in the record representation clause to be in any particular textual order. The offsets alone specify the components' order in memory. A good style, though, is to order the components in the representation clause so that their textual order corresponds to their order in memory. Doing so facilitates our verifying that the layout is correct because the offsets will be increasing as we read the specification.

An individual component may occupy part of a single storage element, all of a single storage element, multiple contiguous storage elements, or a combination of those (i.e., some number of whole storage elements but also part of another). The bit "range" specifies this bit-specific layout, per component, by specifying the first and last bits occupied. The X component occupies 4 complete 8-bit storage elements, so the bit range is 0 through 31, for a total of 32 bits. All the other components each occupy an entire single storage element so their bit ranges are 0 through 7, for a total of 8 bits.

The text specifying the offset and bit range is known as a "component_clause" in the syntax productions. Not all components need be specified by component_clauses, but (not surprisingly) at most one clause is allowed per component. Really none are required but it would be strange not to have some. Typically, all the components are given positions. If component_clauses are given for all components, the record_representation_clause completely specifies the representation of the type and will be obeyed exactly by the implementation.

Components not otherwise given an explicit placement are given positions chosen by the compiler. We don't say that they "follow" those explicitly positioned because there's no requirement that the explicit positions start at offset 0, although it would be unusual not to start there.

Placements must not make components overlap, except for components of variant parts, a topic covered elsewhere. You can also specify the placement of implementation-defined components, as long as you have a name to refer to them. (In addition to the components listed in the source code, the implementation can add components to help implement what you wrote explicitly.) Such names are always attribute references but the specific attributes, if any, are implementation-defined. It would be a mistake for the compiler to define such implicit components without giving you a way to refer to them. Otherwise they might go exactly where you want some other component to be placed, or overlap that place.

The positions (offsets) and the bit numbers must be static, informally meaning that they are known at compile-time. They don't have to be numeric literals, though. Numeric constants would work, but literals are the most common by far.

Note that the language does not limit support for component clauses to specific component types. They need not be one of the integer types, in particular. For example, a position can be given for components that are themselves record types, or array types. Even task types are allowed as far as the language goes, although the implementation might require a specific representation, such as the component taking no bits whatsoever (0 .. -1). There are restrictions that keep things sane, for example rules about how a component name can be used within the overall record layout construct, but not restrictions on the types allowed for individual components. For example, here is a record layout containing a String component, arbitrarily set to contain 11 characters:

type R is record
   S : String (1 .. 11);
   B : Boolean;
end record;

for R use record
   S at 0  range 0 .. 87;
   B at 11 range 0 .. 7;
end record;

Component S is to be the first component in memory in this example, hence the position offset is 0, for the first byte of S. Next, S is 11 characters long, or 88 bits, so the bit range is 0 .. 87. That's 11 bytes of course, so S occupies storage elements 0 .. 10. Therefore, the next component position must be at least 11, unless there is to be a gap, in which case it would be greater than 11. We'll place B immediately after the last character of S, so B is at storage element offset 11 and occupying all that one byte's bits.

We'll have more to say about record type layouts but first we need to talk about alignment.

Modern target architectures are comparatively strict about the address alignments for some of their types. If the alignment is off, an access to the memory for objects of the type can have highly undesirable consequences. Some targets will experience seriously degraded performance. On others, the target will halt altogether. As you can see, getting the alignment correct is a low-level, but vital, part of correct code on these machines.

Normally the compiler does this work for us, choosing an alignment that is both possible for the target and also optimal for speed of access. You can, however, override the compiler's alignment choice using an attribute definition clause or the Alignment aspect. You can do so on types other than record types, but specifying it on record types is typical. Here's our example record type with the alignment specified via the aspect:

type My_Int is range 1 .. 10;

subtype S is Integer range 1 .. 10;

type R is record
   M : My_Int;
   X : S;
   B : Boolean;
   C : Character;
end record with
   Alignment => 1;

Alignment values are in terms of storage elements. The effect of the aspect or attribute clause is to ensure that the starting address of the memory allocated to objects of the type will be a multiple of the specified value.

In fact, whenever we specify a record type layout we really should also specify the record type's alignment, even though doing so is optional. Why? The alignment makes a difference in the overall record object's size. We've seen that already, with the padding bytes: the compiler will respect the alignment requirements of the components, and may add padding bytes within the record and also at the end to ensure components start at addresses compatible with their alignment requirements. The alignment also affects the size allocated to the record type even when the components are already aligned. As a result the overall size could be larger than we want for the sake of space. Additionally, when we pass such objects to code written in other languages, we want to ensure that the starting address of these objects is aligned as the external code expects. The compiler might not choose that required alignment by default.

Specifying alignment for record types is so useful that in the first version of Ada there was no syntax to specify alignment for anything other than record types (via the obsolete at mod clause on record representation clauses).

For that reason GNAT provides a pragma named Optimize_Alignment. This is a configuration pragma that affects the compiler's choice of default alignments where no alignment is explicitly specified. There is a time/space trade-off in the selection of these values, as we've seen. The normal choice tries to balance these two characteristics, but with an argument to the pragma you can give more weight to one or the other. The best approach is to specify the alignments explicitly, per type, for those that require specific alignment values. The pragma has the nice property of giving general guidance to the compiler for what should be done for the other types and objects not explicitly specified.

Now let's look into the details. We'll use a case study for this purpose, including specifying sizes as well as alignments.

The code for the case study is as follows. It uses Size clauses to specify the Sizes, instead of the Size aspect, just to emphasize that the Size clause approach is not obsolete.

package Some_Types is

   type Temperature is range -275 .. 1_000;

   type Identity is range 1 .. 127;

   type Info is record
      T  : Temperature;
      Id : Identity;
   end record;

   for Info use record
      T  at 0 range 0 .. 15;
      Id at 2 range 0 .. 7;
   end record;

   for Info'Size use 24;

   type List is array (1 .. 3) of Info;
   for List'Size use 24 * 3;

end Some_Types;

When we compile this, the compiler will complain that the size for List is too small, i.e., that the minimum allowed is 96 bits instead of the 72 we specified. We specified 24 * 3 because we said the record size should be 24 bits, and we want our array to contain 3 record components of that size, so 72 seems right.

What's wrong? As we've shown earlier, specifying the record type size doesn't necessarily mean that objects (in this case array components) are that size. The object size could be bigger than we specified for the type. In this case, the compiler says we need 96 total bits for the array type, meaning that each of the 3 array components is 32 bits wide instead of 24.

Why is it 32 bits? Because the alignment for Info is 2 (on this machine). The record alignment is a multiple of the largest alignment of the enclosed components. The alignment for type Temperature (2), is larger than the alignment for type Identity (1), therefore the alignment for the whole record type is 2. We need to go from that number of storage elements to a number of bits for the size.

Here's where it gets subtle. The alignment is in terms of storage elements. Each storage element is of a size in bits given by System.Storage_Unit. We've said that on our hypothetical machine Storage_Unit is 8, so storage elements are 8 bits wide on this machine. Bytes, in other words. Therefore, to get the required size in bits, we have to find a multiple of the two 8-bit bytes (specified by the alignment) that has at least the number of bits we gave in the Size clause. Two bytes only provides 16 bits, so that's not big enough, we need at least 24 bits. The next multiple of 2 bytes is 4 bytes, providing 32 bits, which is indeed larger than 24. Therefore, the overall size of the record type, consistent with the alignment, is 4 bytes, or 32 bits. That's why the compiler says each array component is 32 bits wide.

But for our example let's say that we really want to use only 72 total bits for the array type (and that we want three array components). That's the size we specified, after all. So how do we get the record type to be 24 bits instead of 32? Yes, you guessed it, we change the alignment for the record type. If we change it from 2 to 1, the size of 24 bits will work. Adding this Alignment clause line will do that:

for Info'Alignment use 1;

An alignment of 1 means that any address will work, assuming that addresses refer to entire storage elements. (An alignment of 0 would mean that the address need not start on a storage element boundary, but we know of no such machines.)

We can even entirely replace the Size clause with the Alignment clause, because the Size clause specifying 24 bits is just confirming: it's the value that 'Size would return anyway. The problem is the object size.

Now, you may be wondering why an alignment of 1 would work, given that the alignment of the Temperature component is 2. Wouldn't it slow down the code, or even trap? Well, maybe. It depends on the machine. If it doesn't work we would just have to use 32 bits for the record type, with the original alignment of 2, for a larger total array size. Of course, if the compiler recognizes that a representation cannot be supported it must reject the code, but the compiler might not recognize the problem.

We said earlier that there are only a small number of reasons to specify 'Size for a type. We can mention one of them now. Setting 'Size can be useful to give the minimum number of bits to use for a component of a packed composite type, that is, within either a record type or an array type that is explicitly packed via the aspect or pragma Pack. It says that the compiler, when giving its best effort, shouldn't compress components of the type any smaller than the number of bits specified. No, it isn't earth-shattering, but other uses are more valuable, to be discussed soon.

One thing we will leave unaddressed (pun intended) is the question of bit ordering and byte ordering within our record layouts. In other words, the "endian-ness". That's a subject beyond the scope of this course. Suffice it to say that GNAT provides a way to specify record layouts that are independent of the endian-ness of the machine, within some implementation-oriented limits. That's obviously useful when the code might be compiled for a different ISA in the future. On the other hand, if your code is specifically for a single ISA, e.g. Arm, even if different boards and hardware vendors are involved, there's no need to be independent of the endian-ness. It will always be the same in that case. (Those are "famous last words" though.) For an overview of the GNAT facility, an attribute named attribute Scalar_Storage_Order see https://www.adacore.com/papers/lady-ada-mediates-peace-treaty-in-endianness-war.

Although specifying record type layouts and alignments are perhaps the most common representation characteristics expressed, there are a couple of other useful cases. Both involve storage allocation.

One useful scenario concerns tasking. We can specify the number of storage elements reserved for the execution of a task object, or all objects of a task type. You use the Storage_Size aspect to do so:

task Servo with
  Storage_Size => 1 * 1024,
  ...

Or the corresponding pragma:

task Servo is
   pragma Storage_Size (1 * 1024);
end Servo;

The aspect seems textually cleaner and lighter unless you have task entries to declare as well. In that case the line for the pragma wouldn't add all that much. That's a matter of personal aesthetics anyway.

The specified number of storage elements includes the size of the task's stack (GNAT does have one, per task). The language does not specify whether or not it includes other storage associated with the task used for implementing and managing the task execution. With GNAT, the extent of the primary stack size is the value returned, ignoring any other storage used internally in the run-time library for managing the task.

The GNAT run-time library allocates a default stack amount to each task, with different defaults depending on the underlying O.S., or lack thereof, and the target. You need to read the documentation to find the actual amount, or, with GNAT, read the code.

You would need to specify this amount in order to either increase or decrease the allocated storage. If the task won't run properly, perhaps crashing at strange and seemingly random places, there's a decent chance it is running out of stack space. That might also be the reason if you have a really deep series of subprogram calls that fails. The correction is to increase the allocation, as shown above. How much? Depends on the application code. The quick-and-dirty approach is to iteratively increase the allocation until the task runs properly. Then, reverse the approach until it starts to fail again. Add a little back until it runs, and leave it there. We'll mention a much better approach momentarily (GNATstack).

Even if the task doesn't seem to run out of task stack, you might want to reduce it anyway, to the extent possible, because the total amount of storage on your target might be limited. Some of the GNAT bare-metal embedded targets have very small amounts of memory available, so much so that the default task stack allocations would exhaust the memory available quickly. That's what the example above does: empirical data showed that the Servo task could run with just 1K bytes allocated, so we reduced it from the default accordingly. (We specified the size with that expression for the sake of readability, relative to using literals directly.)

Notice we said "empirical data" above. How do we know that we exercised the task's thread of control exhaustively, such that the arrived-at allocation value covers the worst case? We don't, not with certainty. If we really must know the allocation will suffice for all cases, say because this is a high-integrity application, we would use GNATstack. GNATstack is an offline tool that exploits data generated by the compiler to compute worst-case stack requirements per subprogram and per task. As a static analysis tool, its computation is based on information known at compile time. It does not rely on empirical run-time information.

The other useful scenario for allocating storage concerns access types, specifically access types whose values designate objects, as opposed to designating subprograms. (Remember, objects are either variables or constants.) There is no notion of dynamically allocating procedures and functions in Ada so access-to-subprogram types are not relevant here. But objects can be of protected types (or task types), and protected objects can "contain" entries and protected subprograms, so there's a lot of expressive power available. You just don't dynamically allocate procedures or functions as such.

First, a little background on access types, to supplement what we said earlier.

By default, the implementation chooses a standard storage pool for each named access-to-object type. The storage allocated by an allocator (i.e., new) for such a type comes from the associated pool.

Several access types can share the same pool. By default, the implementation might choose to have a single global storage pool, used by all such access types. This global pool might consist merely of calls to operating system routines (e.g., malloc), or it might be a vendor-defined pool instead. Alternatively, the implementation might choose to create a new pool for each access-to-object type, reclaiming the pool's memory when the access type goes out of scope (if ever). Other schemes are possible.

Finally, users may define new pool types, and may override the choice of pool for an access-to-object type by specifying Storage_Pool for the type. In this case, allocation (via new) takes memory from the user-defined pool and deallocation puts it back into that pool, transparently.

With that said, here's how to specify the storage to be used for an access-to-object type. There are two ways to do it.

If you specify Storage_Pool for an access type, you indicate a specific pool object to be used (user-defined or vendor-defined). The pool object determines how much storage is available for allocation via new for that access type.

Alternatively, you can specify Storage_Size for the access type. In this case, an implementation-defined pool is used for the access type, and the storage available is at least the amount requested, maybe more (it might round up to some advantageous block size, for example). If the implementation cannot satisfy the request, Storage_Error is raised.

It should be clear that that the two alternatives are mutually exclusive. Therefore the compiler will not allow you to specify both.

Each alternative has advantages. If your only concern is the total number of allocations possible, use Storage_Size and let the implementation do the rest. However, maybe you also care about the behavior of the allocation and deallocation routines themselves, beyond just providing and reclaiming the storage. In that case, use Storage_Pool and specify a pool object of the appropriate type. For example, you (or the vendor, or someone else) might create a pool type in which the allocation routine performs in constant time, because you want to do new in a real-time application where predictability is essential.

Lastly, an idiom: when using Storage_Size you may want to specify a value of zero. That means you intend to do no allocations whatsoever, and want the compiler to reject the code if you try. Why would you want an access type that doesn't allow dynamically allocating objects? It isn't as unreasonable as it might sound. If you plan to use the access type strictly with aliased objects, never doing any allocations, you can have the compiler enforce your intent. There are application domains that prohibit dynamic allocations due to the difficulties in analyzing their behavior, including issues of fragmentation and exhaustion. Access types themselves are allowed in these domains. You'd simply use them to designate aliased objects alone. In addition, in this usage scenario, if the implementation associates an actual pool with each access type, the pool's storage would be wasted since you never intend to allocate any storage from it. Specifying a size of 0 tells the implementation not to waste that storage.

Before we end this section, there is a GNAT compiler switch you should know about. Th -gnatR? switch instructs the compiler to list the representation details for the types, objects and subprograms in the compiled file(s). Both implementation-defined and user-defined representation details are presented. The '?' is just a placeholder and can be one of the following characters:

[0|1|2|3|4][e][j][m][s]

Increasing numeric values provide increasing amounts of information. The default is '1' and usually will suffice. See the GNAT User's Guide for Native Platforms for the details of the switch in section 4.3.15 Debugging Control.

You'll have to scroll down some to find that specific switch but it is worth finding and remembering. When you cannot understand what the compiler is telling you about the representation of something, this switch is your best friend.

Unchecked Programming

Ada is designed to be a reliable language by default, based as it is on static strong typing and high-level semantics. Many of the pitfalls that a developer must keep in the back of their mind with other languages do not apply in Ada, and are typically impossible. That protection extends to low-level programming as well, e.g., the Separation Principle. Nevertheless, low-level programming occasionally does require mechanisms that allow us to go beyond the safety net provided by the type rules and high-level language constructs.

One such mechanism (unchecked conversion) provides a way to circumvent the type system, a system otherwise firmly enforced by the compiler on our behalf. Note that by "circumventing the type system" we do not include so-called "checked" conversions. These conversions have meaningful semantics, and are, therefore, allowed by the language using a specific syntax. This conversion syntax is known as "functional" syntax because it looks like a function call, except that the "function" name is a type name, and the parameter is the object or value being converted to that type. These conversions are said to be "checked" because only specific kinds of types are allowed, and the compiler checks that such conversions are indeed between these allowed types.

Instead, this section discusses "unchecked" programming, so-called because the compiler does not check for meaningful semantics. There are multiple mechanisms for unchecked programming in Ada: in addition to circumventing the type system, we can also deallocate a previously-allocated object, and can create an access value without the usual checks. In all cases the responsibility for correct meaning and behavior rests on the developer. Very few, if any, checks are done by the compiler. If we convert a value to another type that generally makes no sense, for example a task object converted to a record type, we are on our own. If we deallocate an allocated object more than once, it is our fault and Bad Things inevitably result.

Likened to "escape hatches," the facilities for unchecked programming are explicit in Ada. Their use is very clear in the source code, and is relatively heavy: each mechanism is provided by the language in the form of a generic library subprogram that must be specified in a context clause ("with-clause") at the top of the file, and then instantiated prior to use, like any generic. For an introduction to generic units in Ada, see that section in the introductory Ada course: Introduction to Ada

You should understand that the explicitly unchecked facilities in Ada are no more unsafe than the implicitly unchecked facilities in other languages. There's no safety-oriented reason to "drop down" to C, for example, to do low-level programming. For that matter, the low-level programming facilities in Ada are at least as powerful as those in other languages, and probably more so.

We will explore unchecked storage deallocation in a separate book so let's focus on unchecked type conversions.

Unchecked type conversions are achieved by instantiating this language-defined generic library function, a "child" of the root package named "Ada":

generic
   type Source(<>) is limited private;
   type Target(<>) is limited private;
function Ada.Unchecked_Conversion (S : Source) return Target
   with Pure, Nonblocking, Convention => Intrinsic;

The function, once instantiated and eventually invoked, returns the caller's value passed to S (of type Source) as if it is a value of type Target. That value can then be used in any way consistent with the Target type.

The two generic parameters, Source and Target, are defined in a manner that makes them very permissive in terms of the types they will accept when instantiated. To understand how, you need to understand a little bit of Ada's terminology and design for generic unit parameters. (If you are already familiar with generic formal types and how they are matched, feel free to skip this material.)

First, the terminology. The type parameters defined by a generic unit are known as "generic formal types," or "generic formals" for short. Types Source and Target are the generic formals in the unit above. When instantiating such a generic, clients must specify a type for each generic formal type. The types specified by the client are known as "generic actual types," or "generic actuals" for short. You can remember that by the fact that the actuals are the types "actually" given to the generic unit to work with when instantiated. (You may laugh, but that mnemonic works.)

Now we're ready to discuss the language design concept. The idea is that the syntax of a generic formal type indicates what kind of generic actual is required for a legal instantiation. This is known as the "Contract Model" because we can think of the formal parameters as expressing a contract between the generic unit's implementation and the client code that instantiates the generic. The contract is enforced by the compiler, in that it will reject any instantiation that attempts to specify some actual type that does not match the formal's requirements.

For example, if the generic computes some value for any floating point type, that floating-point type would be declared as a generic formal type, and would be defined so that only some floating-point type could be used for the corresponding actual type:

generic
   type Real is digits <>;

The formal parameter syntax reflects the syntax of a floating-point type declaration, except that the <> (the "box") indicates that the generic does not care how many digits are available. The generic actual will be some floating point type and it will specify the number of decimal digits.

If instead we try to match that formal with some actual that is anything other than a floating-point type the compiler will reject the instantiation. Therefore, within the generic body, the implementation code can be written with the assurance that the characteristics and capabilities required of a floating point type will be available. That's the Contract Model in full: the requirements are a matter of the generic unit's purpose and implementation, so the formal parameters reflect those requirements and the compiler ensures they will be met.

Some generic units, though, do not require specifically numeric actual types. These generics can use less specific syntax for their formal types, and as a result, more kinds of actual types are permitted in the instantiations. Remember the Contract Model and this will make sense. The contract between the generic and the clients is, in this case, more permissive: it does not require a numeric type in order to implement whatever it does.

For illustration, suppose we want a generic procedure that will exchange two values of some type. What operations does the generic unit require in the implementation in order to swap two values? There are two: assignment, as you might expect, but also the ability to declare objects of the type (the "temporary" used to hold one of the values during the swap steps). As long as the body can do that, any type will suffice, so the generic formals are written to be that permissive. What is the syntax that expresses that permissiveness, you ask? To answer that, first consider simple, non-generic private types from the user's point of view. For example:

package P is
   type Foo is private;
   procedure Do_Something (This : Foo);
private
   type Foo is ...  -- whatever
end P;

There are two "views" associated with the package: one for the "visible" part of the package spec (declaration), known as the "partial" view, and one for the "private" part of the package spec and the package body, known as the "full" view. The differences between the two views are a function of compile-time visibility.

The partial view is what clients (i.e., users) of the package have: the ability to do things that a type name provides, such as declarations of objects, as well as some basic operations such as assignment, some functions for equality and inequality, some conversions, and whatever subprograms work on the type (the procedure Do_Something above). Practically speaking, that's about all that the partial view provides. That's quite a lot, in fact, and corresponds to the classic definition of an "abstract data type."

The code within the package private part and package body has the full view. This code has compile-time visibility to the full definition for type Foo, so there are additional capabilities available to this code. For example, if the full definition for Foo is as an array type, indexing will be available with the private part and body. If Foo is fully defined as some numeric type, arithmetic operations will be possible within the package, and so on.

Therefore, the full view provides capabilities for type Foo that users of the type cannot access via the partial view. Only the implementation for type Foo and procedure Do_Something have the potential to access them.

Now, back to the generic formal parameter. If the generic unit doesn't care what the actual type is, and just needs to be able do assignment and object declaration, a "generic formal private type" expresses exactly that:

generic
   type Item is private;
procedure Exchange( Left, Right : in out Item );

procedure Exchange( Left, Right : in out Item ) is
   Old_Left : Item;
begin
   Old_Left := Left;
   Left := Right;
   Right := Old_Left;
end Exchange;

Inside generic procedure Exchange, the view of type Item is as if Item were some private type declared in a package, with only the partial view available. But the operations provided by a partial view are sufficient to implement the body of Exchange: only assignment and object declaration are required. Any additional capabilities that the generic actual type may have — array indexing, arithmetic operators, whatever — are immaterial because they are not required. That's the Contract Model: only the specified view's required capabilities are important. Anything else the type can also do is not relevant.

But consider limited types. Those types don't allow assignment, by definition. Therefore, an instantiation that specified a limited actual type for the generic formal type Item above would be rejected by the compiler. The contract specifies the ability to do assignment so a limited type would violate the contract.

Finally, as mentioned, our Exchange generic needs to declare the "temporary" object Old_Left. A partial view of a private type allows that. But not all types are sufficient, by their name alone, to declare objects. Unconstrained array types, such as type String, are a familiar example: they require the bounds to be specified when declaring objects; the name String alone is insufficient. Therefore, such types would also violate the contract and, therefore, would be rejected by the compiler when attempting to instate generic procedure Exchange.

Suppose, however, that we have some other generic unit whose implementation does not need to declare objects of the formal type. In that case, a generic actual type that did not support object declaration (by the name alone) would be acceptable for an instantiation. The generic formal syntax for expressing that contract uses these tokens: (<>) in addition to the other syntax mentioned earlier:

generic
   type Foo(<>) is private;

In the above, the generic formal type Foo expresses the fact that it can allow unconstrained types — known as "indefinite types" — when instantiated because it will not attempt to use that type name to declare objects. Of course, the compiler will also allow constrained types (e.g., Integer, Boolean, etc.) in instantiations because it doesn't matter one way or the other inside the generic implementation. The Contract Model says that additional capabilities, declaring objects in this case, are allowed but not required. (There is a way to declare objects of indefinite types, but not using the type name alone. The unchecked facilities don't need to declare objects so we will not show how to do it.)

Now that you understand the Contract Model (perhaps more than you cared), we are ready to examine the generic formal type parameters for Ada.Unchecked_Conversion. Here's the declaration again:

generic
   type Source(<>) is limited private;
   type Target(<>) is limited private;
function Ada.Unchecked_Conversion (S : Source) return Target
   with Pure, Nonblocking, Convention => Intrinsic;

The two generic formal types, Source, and Target, are the types used for the incoming value and the returned value, respectively. Both formals are "indefinite, limited private types" in the jargon, but now you know what that means. Inside the implementation of the generic function, neither Source nor Target will be used to declare objects (the (<>) syntax). Likewise, neither type will be used in an assignment statement (the "limited" reserved word). And finally, no particular kind of type is required for Source or Target (the private reserved word). That's a fairly restricted usage within the generic implementation, but as a result the contract can be very permissive: the generic can be instantiated with almost any type. It doesn't matter if the actual is limited or not, private or not, and indefinite or not. The generic implementation doesn't need those capabilities to implement a conversion so they are not part of the contract expressed by the generic formal types.

What sort of type would be disallowed? Abstract types, and incomplete types. However, it is impossible to declare objects of those types, for good reasons, so unchecked conversion is never needed for them.

Note that the result value is returned by-reference whenever possible, in which case it is just a view of the Source bits in the formal parameter S and not a copy. For a Source type that is not a by-copy type, the result of an unchecked conversion will typically be returned by-reference (so that the result and the parameter S share the same storage); for a by-copy Source type, a copy is made.

The compiler can restrict instantiations but implementers are advised by the language standard to avoid them unless they are required by the target environment. For example, an instantiation for types for which unchecked conversion can't possibly make sense might be disallowed.

Clients can apply language- and vendor-defined restrictions as well, via pragma Restrictions. In particular, the language defines the No_Dependence restriction, meaning that no client's context clause can specify the unit specified. As a result no client can instantiate the generic for unchecked conversion:

pragma Restrictions (No_Dependence => Ada.Unchecked_Conversion);

hence there would be no use of unchecked conversion.

From the Contract Model's point of view most any type can be converted to some other type via this generic function. But practically speaking, some limitations are necessary. The following must all be true for the conversion effect to be defined by the language:

• S'Size = Target'Size

• S'Alignment is a multiple of Target'Alignment, or Target'Alignment is 0 (meaning no alignment required whatsoever)

• Target is not an unconstrained composite type

• S and Target both have a contiguous representation

• The representation of S is a representation of an object of the target subtype

We will examine these requirements in turn, but realize that they are not a matter of legality. Compilers can allow instantiations that violate these requirements. Rather, they are requirements for conversions to have the defined effect.

The first requirement is that the size (in bits) for the parameter S, of type Source, is the same as the size of the Target type. That's reasonable if you consider it. What would it mean to convert, for example, a 32-bit value to an 8-bit value? Which 8 bits should be used?

As a result, one of the few reasons for setting the size of a type (as opposed to the size of an object) is for the sake of well-defined unchecked conversions. We might make the size larger than it would need to be because we want to convert a value of that type to what would otherwise be a larger Target type.

Because converting between types that are not the same size is so open to interpretation, most compilers will issue a warning when the sizes are not the same. Some will even reject the instantiation. GNAT will issue a warning for these cases when the warnings are enabled, but will allow the instantiation. We're supposed to know what we are doing, after all. The warning is enabled via the specific -gnatwz switch or the more general -gnatwa switch. GNAT tries to be permissive. For example, in the case of discrete types, a shorter source is first zero or sign extended as necessary, and a shorter target is simply truncated on the left. See the GNAT RM for the other details.

The next requirement concerns alignment. As we mentioned earlier, modern architectures tend to have strict alignment requirements. We can meaningfully convert to a type with a stricter alignment, or to a type with no alignment requirement, but converting in the other direction would require a copy.

Next, recall that objects of unconstrained types, such as unconstrained array types or discriminated record types, must have their constraints specified when the objects are declared. We cannot just declare a String object, for example, we must also specify the lower and upper bounds. Those bounds are stored in memory, logically as part of the String object, since each object could have different bounds (that's the point, after all). What, then, would it mean to convert some value of a type that has no bounds to a type that requires bounds? The third requirement says that it is not meaningful to do so.

The next requirement is that the argument for S, and the conversion target type Target, have a contiguous representation in memory. In other words, each storage unit must be immediately adjacent, physically, to the next logical storage unit in the value. Such a representation for any given type is not required by the language, although on typical modern architectures it is common. (The type System.Storage_Elements.Storage_Array is an exception, in that a contiguous representation is guaranteed.) An instance of Ada.Unchecked_Conversion just takes the bits of S and treats them as if they are bits for a value of type Target (more or less), and does not handle issues of segmentation.

The last requirement merely states that the bits of the argument S, when treated as a value of type Target, must actually be a bit-pattern representing a value of type Target (strictly, the subtype). For example, with signed integers, any bit pattern (of the right size) represents a valid value for those types. In contrast, consider an enumeration type. By default, the underlying representational values are the same as the position values, i.e., starting at zero and increasing by one. But users can override that representation: they can start with any value and, although the values must increase, they need not increase by one:

type Toggle_Switch is (Off, On);
for Toggle_Switch use (Off => 0, On => 4);

If we covert an unsigned integer (of the right size) to a Toggle_Switch value, what would it mean if the Source value was neither 0 nor 4?

We've said that the instantiations are likely allowed, hence callable functions are created. If the above requirements are not met, what happens?

What happens depends on the Target type, that is, the result type for the conversion. Specifically, it depends on whether the target type is a "scalar" type. As we mentioned earlier, a scalar type is either a "discrete" type or a "real" type, which are themselves further defined, as the figure below indicates. Any other type is a non-scalar type, e.g., record types, access types, task types, and so on.

When the requirements for meaningful instantiations are not respected and the Target type is a scalar type, the result returned from the call is implementation defined and is potentially an invalid representation. For example, type Toggle_Switch is an enumeration type, hence it is a scalar type. Therefore, if we covert an unsigned integer (of the right size) to a Toggle_Switch value, and the Source value is neither 0 nor 4, the resulting value is an invalid representation. That's the same as an object of type Toggle_Switch that is never assigned a value. The random junk in the bits may or may not be a valid Toggle_Switch value. That's not a good situation, clearly, but it is well-defined: if it is detected, either Constraint_Error or Program_Error is raised. If the situation is not detected, execution continues using the invalid representation. In that case it may or may not be detected, near the call or later. For example:

with Ada.Unchecked_Conversion;
with Ada.Text_IO;  use Ada.Text_IO;
with Interfaces;   use Interfaces;

procedure Demo is

   type Toggle_Switch is (Off, On) with Size => 8;
   for Toggle_Switch use (Off => 1, On => 4);

   function As_Toggle_Switch is new Ada.Unchecked_Conversion
     (Source => Unsigned_8, Target => Toggle_Switch);

   T1 : Toggle_Switch;
   T2 : Toggle_Switch;
begin
   T1 := As_Toggle_Switch (12);  -- neither 1 nor 4
   if T1 = Off then
      Put_Line ("T1's off");
   else
      Put_Line ("T1's on");
   end if;
   T2 := T1;
   if T2 = Off then
      Put_Line ("T2's off");
   else
      Put_Line ("T2's on");
   end if;
   Put_Line (T2'Image);
end Demo;

In the execution of the code above, the invalid representation value in T1 is not detected, except that it is copied into T2, where it is eventually detected when 'Image is applied to T2. The invalid representation is not detected in the assignment statement or the comparison because we want the optimizer to be able to avoid emitting a check prior to every use of the value. Otherwise the generated code would be too slow. (The language explicitly allows this optimization.)

The evaluation of an object having an invalid representation value due to unchecked conversion is a so-called "bounded error" because the results at run-time are predictable and limited to one of those three possibilities: the two possible exceptions, or continued execution.

Continued execution might even work as hoped, but such code is not portable and should be avoided. A new vendor's compiler, or even a new version of a given vendor's compiler, might detect the situation and raise an exception. That happens, and it ends up costing developer time to make the required application code changes.

The possibilities get much worse when the result type is not a scalar type. In this case, the effect of the call — not the value returned by the call — is implementation defined. As a result, the possible run-time behavior is unpredictable and, consequently, from the language rules point of view anything is possible. Such execution is said to be "erroneous."

Why the difference based on scalar versus non-scalar types? Scalar types have a simple representation: their bits directly represent their values. Non-scalar types don't always have a simple representation that can be verified by examining their bits.

For example, we can have record types with discriminants that control the size of the corresponding objects because the record type contains an array component that uses the discriminant to set the upper bound. These record types might have multiple discriminants, and multiple dependent components. As a result, an implementation could have hidden, internal record components. These internal components might be used to store the starting address of the dependent components, for example, or might use pointers to provide a level of indirection. If an unchecked conversion did not provide correct values for these internal components, the effect of referencing the record object would be unpredictable.

Even a comparatively simple record type with one such dependent component is sufficient to illustrate the problem. There are no internal, hidden components involved:

with Ada.Unchecked_Conversion;
with Ada.Text_IO;             use Ada.Text_IO;
with System;                  use System;  -- for Storage_Unit
with System.Storage_Elements; use System.Storage_Elements;

procedure Demo_Erroneous is

   subtype Buffer_Size is Storage_Offset range 1 .. Storage_Offset'Last;

   type Bounded_Buffer (Capacity : Buffer_Size) is record
      Content : Storage_Array (1 .. Capacity);
      Length  : Storage_Offset := 0;
   end record;

   procedure Show_Capacity (This : Bounded_Buffer);

   subtype OneK_Bounded_Buffer is Bounded_Buffer (Capacity => 1 * 1024);

   function As_OneK_Bounded_Buffer is new Ada.Unchecked_Conversion
     (Source => Storage_Array, Target => OneK_Bounded_Buffer);

   Buffer   : OneK_Bounded_Buffer;
   Sequence : Storage_Array (1 .. Buffer'Size / Storage_Unit);

   procedure Show_Capacity (This : Bounded_Buffer) is
   begin
      Put_line ("This.Capacity is" & This.Capacity'Image);
   end Show_Capacity;

begin
   Buffer := As_OneK_Bounded_Buffer (Sequence);
   Put_Line ("Buffer capacity is" & Buffer.Capacity'Image);
   Show_Capacity (Buffer);
   Put_Line ("Done");
end Demo_Erroneous;

In the above, the type Bounded_Buffer has an array component Content that depends on the discriminant Capacity for the number of array components. This is an extremely common idiom. However, unchecked conversion is only meaningful, as defined earlier, when converting to constrained target types. Bounded_Buffer is not constrained, so we define a constrained subtype (OneK_Bounded_Buffer) for the sake of the conversion.

The specific Buffer object is 8320 bits (1024 * 8, plus 2 * 64), as is the Sequence object, so the sizes are the same.

The alignment of OneK_Bounded_Buffer is 8, and Storage_Array's alignment is 1, so the Target type is a multiple of the Source type, as required.

Both types have a contiguous representation, and the sequence of bytes can be a valid representation for the record type, although it certainly might not be valid. For example, if we change the discriminant from what the subtype specifies, we would have an invalid representation for that subtype.

So we can reasonably invoke an unchecked conversion between the array of bytes and the record type. However, as you can see in the code and as the compiler warns, we never assigned a value to the Sequence array object. The unchecked conversion from that Sequence of bytes includes the discriminant value, so it is very possible that we will get a discriminant value that is not 1K.

We can test that possibility by running the program. In the first call to Put_Line, the program prints the Capacity discriminant for the Buffer object. The compiler knew it was 1024, so it doesn't get the discriminant component from memory, it just directly prints 1024. However, we can force the compiler to query the discriminant in memory. We can pass Buffer to procedure Show_Capacity, which takes any Bounded_Buffer, and there query (print) the Capacity component under that different view. That works because the view inside the procedure Show_Capacity is as of Bounded_Buffer, in which the discriminant value is unknown at compile-time.

In the above examples, we are responsible for ensuring that the enumeration representation encoding and the record discriminant value are correct when converted from some other type. That's not too hard to recognize because we can literally see in the source code that there is something to be maintained by the conversions. However, there might be hidden implementation artifacts that we cannot see in the source code but that must be maintained nevertheless.

For example, the compiler's implementation for some record type might use dynamic memory allocations instead of directly representing some components. That would not appear in the source code. As a simpler example of invisible implementation issues, consider again our earlier record type:

As we discussed earlier, between the bytes that are allocated to the record components are some other bytes that are not used at all. As usual, the compiler must implement the language-defined equality operator for the record type. One way to implement that function would be to generate code that checks the equality for each component individually, ignoring any unused bytes. But suppose you have a large record type with many components. The code for checking record level equality will be extensive and inefficient. An alternative implementation for the compiler would be to use a "block compare" machine instruction to check the equality of the entire record at once, rather than component-by-component. That will be considerably more efficient because the block-compare instruction just compares the bits from one starting address to another ending address. But in that case the "unused" bytes are not skipped so the values within those bytes become significant. Comparison of those unused bytes will only work if their values are defined and assigned in each record object. Compilers that may use a block-comparison approach will, therefore, always set those unused bytes to a known value (typically zero). That is part of the valid representation for values of the type, and consequently must be maintained by our unchecked conversions. This being a non-scalar target type, failure to do so results in erroneous execution, i.e., undefined behavior. "There be dragons" as ancient maps of the unknown world once said.

As you can see, you should use unchecked conversions with considerable care and thought. Moreover, because unchecked programming is such a low-level activity, and has vendor-defined implementation issues, it is not only less portable than high-level coding, it is also less portable than other low-level programming. You will be well served if you limit the use of unchecked conversions overall. If your application code is performing unchecked conversions all over the code, something is very likely wrong, or at least very questionable. A well-designed Ada program should not need ubiquitous unchecked conversions.

That said, of course sometimes unchecked conversions are reasonable. But even then, it is better to isolate and hide their use via compile-time visibility controls. For example, instead of having clients invoke unchecked conversion instances many times, have a procedure that is invoked many times, and let the procedure body do the conversion. That way, the clients see a high-level specification of functionality, and, if the conversion needs to be changed later, there is only that one conversion usage (the procedure body) to change. This approach is really just another example of isolating and hiding code that might need to change in the future.

Data Validity

Our earlier demo program assigned an incorrect value via unchecked conversion into an object of an enumeration type that had non-standard representation values. The value assigned was not one of those representation values so the object had an invalid representation. Certain uses of an invalid representation value will be erroneous, and we saw that the effect of erroneous execution was unpredictable and unbounded.

That example was somewhat artificial, for the sake of illustration. But we might get an invalid value in a real-world application. For example, we could get an invalid value from a sensor. Hardware sensors are frequently unreliable and noisy. We might get an invalid value from a call to an imported function implemented in some other language. Whenever an assignment is aborted, the target of the assignment might not be fully assigned, leading to so-called "abnormal" values. Other causes are also possible. The problem is not unusual in low-level programming.

How do we avoid the resulting bounded errors and erroneous execution?

In addition to assignment statements, we can safely apply the Valid attribute to the object. This language-defined attribute returns a Boolean value indicating whether or not the object's value is a valid representation for the object's subtype. (More details in a moment.) There is no portable alternative to check an object's validity. Here's an example:

with Ada.Unchecked_Conversion;
with Ada.Text_IO;  use Ada.Text_IO;
with Interfaces;   use Interfaces;
with System;

procedure Demo_Validity_Check is

   type Toggle_Switch is (Off, On) with Size => 8;
   for Toggle_Switch use (Off => 1, On => 4);

   T1 : Toggle_Switch;

   function Sensor_Reading (Default : Toggle_Switch) return Toggle_Switch is

      function As_Toggle_Switch is new Ada.Unchecked_Conversion
        (Source => Unsigned_8, Target => Toggle_Switch);

      Result : Toggle_Switch;
      Sensor : Unsigned_8;
      --  for Sensor'Address use System'To_Address (...);

   begin
      Result := As_Toggle_Switch (Sensor);
      return (if Result'Valid then Result else Default);
   end Sensor_Reading;

begin
   T1 := Sensor_Reading (Default => Off); -- arbitrary
   Put_Line (T1'Image);
end Demo_Validity_Check;

In the above, Sensor_Reading is the high-level, functional API provided to clients. The function hides the use of the unchecked conversion, and also hides the memory-mapped hardware interface named Sensor. We've commented out the address clause since we don't really have a memory mapped device available. You can experiment with this program by changing the code to assign a value to Sensor (e.g., when it is declared). It is an unsigned 8-bit quantity so any value in the corresponding range would be allowed.

In addition to checking for a valid representation, thus preventing the bounded error, Valid also checks that the object is not abnormal, so erroneous execution can be prevented too. (It also checks that any subtype predicate defined for the Target type is also satisfied, but that's a lesson for another day.)

However, the Valid attribute can be applied only to scalar objects. There is no language-defined attribute for checking objects of composite types. That's because it would be very hard to implement for some types, if not impossible. For example, given a typical run-time model, it is impossible to check the validity of an access value component. Therefore, you must individually check the validity of scalar record or array components.

At least, you would have to check them individually in standard Ada. GNAT defines another Boolean attribute, named Valid_Scalars, to check them all for us. This attribute returns True if the evaluation of Valid returns True for every scalar subcomponent of the enclosing composite type. It also returns True when there are no scalar subcomponents. See the GNAT RM for more information.